回归模型怎么分析

回归模型是用来做预测的。大部分回归分析模型都是连续型预测（逻辑回归除外）。本文介绍只有一个变量的简单线性回归分析方法。

以共享单车服务满意分数据为案例进行模型实战，分析不同的特征对满意分的影响程度，模型过程如下：

1、读取数据

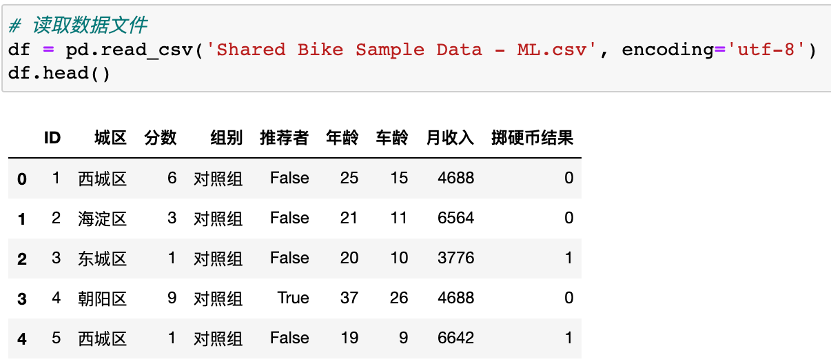
2、切分因变量和自变量、分类变量转换哑变量

3、使用VIF去除多重共线性

多重共线性：就是在线性回归模型中，存在一对以上强相关变量，多重共线性的存在，会误导强相关变量的系数值。

强相关变量：如果两个变量互为强相关变量，当一个变量变化时，与之相应的另一个变量增大/减少的可能性非常大。

当我们加入一个年龄强相关的自变量车龄时，通过最小二乘法所计算得到的各变量系数如下，多重共线性影响了自变量车龄、年龄的线性系数。

这时候，可以使用VIF消除多重共线性：VIF=1/(1-R方)，R方是拿其他自变量去线性拟合此数值变量y得到的线性回归模型的决定系数。某个自变量造成强多重共线性判断标准通常是：VIF>10

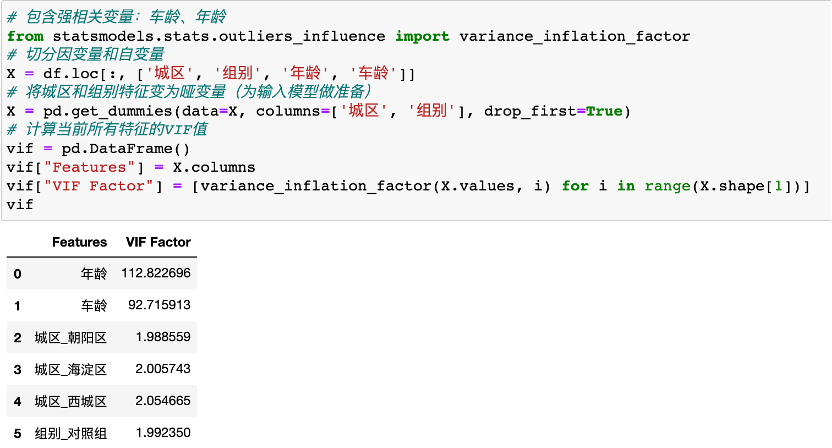
我们发现，年龄的VIF远大于10，故去除年龄这一变量，去除后重新计算剩余变量VIF发现所有均<10，即可继续。

4、计算调整R方

5、数据标准化

我们希望不同自变量的线性系数，相互之间有可比性，不受它们取值范围影响

6、拟合模型，计算回归系数

共享单车分数案例，因变量是分数，自变量是年龄、组别、城区，线性回归的结果为：分数 = 5.5 + 2.7 * 年龄 +0.48 * 对照组 + 0.04 * 朝阳区 + 0.64 * 海淀区 + 0.19 * 西城区

7、生成分析洞见-驱动力因素

最终产出不同用户特征对用户调研分数的驱动性排名。驱动力分数反应各个变量代表因素，对目标变量分数的驱动力强弱，驱动力分数绝对值越大，目标变量对因素的影响力越大，反之越小，驱动力分数为负时，表明此因素对目标变量的影响为负向。

8、根据回归模型进行预测

至此，回归模型已经建好，把要预测的数据x自变量导入模型即可预测y。

---

最后，推荐我们的管理工具给大家