二分查找不能用于链表的原因:二分查找是一种高效的查找算法,适用于已排序且静态的数组或列表,而链表不支持随机内存访问,即每一个节点的地址不能在O(1)的时间复杂度内获得,因此二分查找不能使用于链表。
一、二分查找不能用于链表的原因
链表的每一个节点的地址不能在O(1)的时间复杂度内获得,二分查找是一种高效的查找算法,适用于已排序且静态的数组或列表。然而,二分查找不能使用于链表,因为链表不支持随机内存访问。如下图,名列前茅行是地址,第二行是数组(顺序表),第三行是链表。
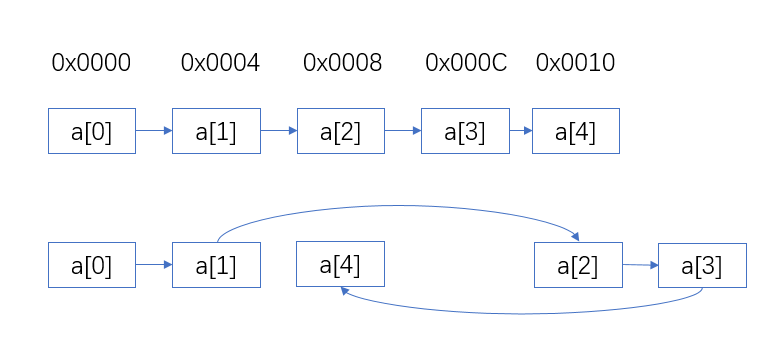
可以看到,在数组(线性表)中,a[i]的地址就是 &a[0]+sizeof(int)*i (a+i),这样你对于一次二分查找 [l,r) 区域,通过简单的计算得到中间值 mid = (l+r)/2 对应的值而对于链表,每个节点对应的坐标是不确定的,比如查找 [0,4) ,需要比较mid = (0+4)/2 = 2 的值,然后电脑就开始找,从0开始往后找到1,找到1再往下找,遍历很多次之后才能找到 a[2] 位于0x0010 这个地址,理论而言,我们每次都需要遍历整个查询区域二分之一长度的数据,即 T(n/2) 。再加上二分查找本身的 T(logn) 总的时间复杂度是 O(nlogn) 甚至比直接遍历链表查询更慢。
二、二分查找的原理及实现
二分查找的实现原理非常简单,首先要有一个有序的列表。但是如果没有,则该怎么办?可以使用排序算法进行排序。以升序数列为例,比较一个元素与数列中的中间位置的元素的大小,如果比中间位置的元素大,则继续在后半部分的数列中进行二分查找;如果比中间位置的元素小,则在数列的前半部分进行比较;如果相等,则找到了元素的位置。每次比较的数列长度都会是之前数列的一半,直到找到相等元素的位置或者最终没有找到要找的元素。
我们先来想象一下,如果数列中有 3 个数,则先与第 2 个数进行比较,如果比第 2 个数大,则与第 2 个数右边的数列进行二分查找,这时这个数列就剩下一个数了,直接比较是否相等即可。所以在 3 个数的时候非常多比较两次。同理,在有 4 个数的时候,我们与中间数进行比较,一般中间数是首加末除以 2 算出来的,这时我们算出来的中间数是 (1+4)/2 等于 2,所以我们把要查找的数与第 2 个数比较,若比第 2 个数小,则直接与第 1 个数比较;否则与后面两个数进行二分查找,这时的中间数是 (3+4)/2 等于 3,也就是后半部分的第 1 个数。再接着进行比较,相等则找到相应的元素,小于则没有这个数(因为左边所有的数都已经判断过了),大于则继续向右查找。所以在 4 个数的时候非常多比较 3 次。以此类推,在 5 个数的时候非常多查找 3 次,在 6 个数的时候也是非常多查找 3 次。
实现代码
public class BinarySearch {
private int[] array;
/**
* 递归实现二分查找
* @param target
* @return
*/
public int searchRecursion(int target) {
if (array != null) {
return searchRecursion(target, 0, array.length - 1);
}
return -1;
}
private int searchRecursion(int target, int start, int end) {
if (start > end) {
return -1;
}
int mid = start + (end - start) / 2;
if (array[mid] == target) {
return mid;
} else if (target < array[mid]) {
return searchRecursion(target, start, mid - 1);
} else {
return searchRecursion(target, mid + 1, end);
}
}
}三、链表简介
1、链表概念
链表是一种常见的基础数据结构,结构体指针在这里得到了充分的利用。链表可以动态的进行存储分配,也就是说,链表是一个功能极为强大的数组,他可以在节点中定义多种数据类型,还可以根据需要随意增添,删除,插入节点。链表都有一个头指针,一般以head来表示,存放的是一个地址。链表中的节点分为两类,头结点和一般节点,头结点是没有数据域的。
2、链表的构成
链表中每个节点都分为两部分,一个数据域,一个是指针域。说到这里你应该就明白了,链表就如同车链子一样,head指向名列前茅个元素:名列前茅个元素又指向第二个元素,直到最后一个元素,该元素不再指向其它元素,它称为“表尾”,它的地址部分放一个“NULL”(表示“空地址”),链表到此结束。作为有强大功能的链表,对他的操作当然有许多,比如:链表的创建,修改,删除,插入,输出,排序,反序,清空链表的元素,求链表的长度等等。
3、常见的链表
- 单链表
- 循环链表
- 双向链表
4、链表的增删改查
我们在进行数组的插入、删除操作的时候,为了保持内存数据的连续性,需要进行大量的数据搬移工作,所以时间复杂度为 O(n);而在链表中插入或者删除一个数据我们并不需要为了保持内存的连续性而搬移节点,因为链表本身的存储空间也不是连续的,所以在链表中插入和删除一个数据是非常快的。
- 插入数据: 我们只需要将要插入位置的前一个数据单元的next指针指向插入数据的内存地址,插入数据的next指针指向下一个数据的内存地址;
- 删除数据: 将要删除数据的前一个数据单元的next指针指向要删除数据的下一个数据单元的内存地址,然后再删除数据。
5、实现代码
public class MyLinkedList<E> {
10 /**
11 * 私有的 Node
12 */
13 private class Node{
14 public E e;
15 public Node next;
16
17 public Node(E e, Node next){
18 this.e = e;
19 this.next = next;
20 }
21 public Node(E e){
22 this(e, null);
23 }
24 public Node(){
25 this(null, null);
26 }
27 }
28 private Node head;
29 private int size;
30
31 public MyLinkedList(){
32 head = null;
33 size = 0;
34 }
35 public int getSize(){
36 return this.size;
37 }
38 public boolean isEmpty(){
39 return size == 0;
40 }
41 }延伸阅读
循环链表简介
- 单向循环链表 [Circular Linked List] : 由各个内存结构通过一个指针 Next 链接在一起组成,每一个内存结构都存在后继内存结构,内存结构由数据域和 Next 指针域组成。
- 双向循环链表 [Double Circular Linked List] : 由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成,每一个内存结构都存在前驱内存结构和后继内存结构,内存结构由数据域、Prev 指针域和 Next 指针域组成。
文章包含AI辅助创作:二分查找为什么不能用于链表,发布者:Z, ZLW,转载请注明出处:https://worktile.com/kb/p/49385

 微信扫一扫
微信扫一扫  支付宝扫一扫
支付宝扫一扫 